Count the number of digits in an integer

Table of Contents

It’s easy to count the characters in a char array or a string but it’s a little tricky to count the number of digits \((k)\) in an integer \((n)\).

The simple \(O(n)\) solution in C:

#include<stdio.h>
int count\_digits(int n){
    int k=0;
    if(n==0){
        return 1;
    }
    while(n!=0){
        n=n/10;
        k++;
    }
    return k;
}
int main(void){
    int n;
    printf("Enter a no.: ");
    scanf("%d", &n);
    printf("Number of digits: %d", count\_digits(n));
    return 0;
}

We can do it in logarithmic time.

It’s time to go mathematical
#

We know that a binary number has base 2 and uses digits 0 and 1, and a decimal number has base 10 and uses digits from 0 to 9.

Now, let’s take a decimal number, say, \(n = 4591\).

We can represent it as, \[4591 = 4 * 10^3 + 5 * 10^2 + 9 * 10^1 + 1 * 10^0\]

Here, the maximum exponent of 10 is 3 to which if we add 1, we get the total no. of digits \((k)\) in integer \(n\) i.e. 4.

We know a logarithm is an inverse function of exponentiation. That means the logarithm of a given no. \(n\) is the exponent to which another fixed number, the base \(b\), must be raised, to produce that no. \(n\).

\[b^{\log_b n} = n\\ or, b^y = n\\ where, y = {\log_b n}\] For example, if \(b = 2, y = 5\ \&\ n = 32\), \[b^y = n\\ 2^5 = 32\\ and, \log_{2} 32 = 5\]

To put it simply, logarithm counts repeated multiplication of the same factor. Logarithm answers the question ‘How many of one number do we multiply to get another number?’. The answer here is we multiplied the no. 2 by itself 5 times to get another no. 32.

Take another example, when \(b = 10, y = 4\ \&\ n = 10,000\), \[b^y = n\\ 10^4 = 10,000\\ and, {\log_{10} 10,000} = 4\]

The interesting thing is we use \(\log_{10}\) for counting the no. of digits \((k)\) in an integer \((n)\). \(\log_{10}\) tries to find the no. of times \(n\) can be divided by 10 until the value of n is less than 10. The value of \({\log_{10} n}\) always turns out to be less than \(k\).

The reason for the value of \(({\log_{10} n}) < k\) can be explained using a simple number line representation. We can place \(n = 4591\) between 1000 and 10,000 since 1000 < 4591 < 10,000 , and the corresponding value of \({\log_{10} 4591}\) turns out to be between 3 and 4 i.e 3.661.

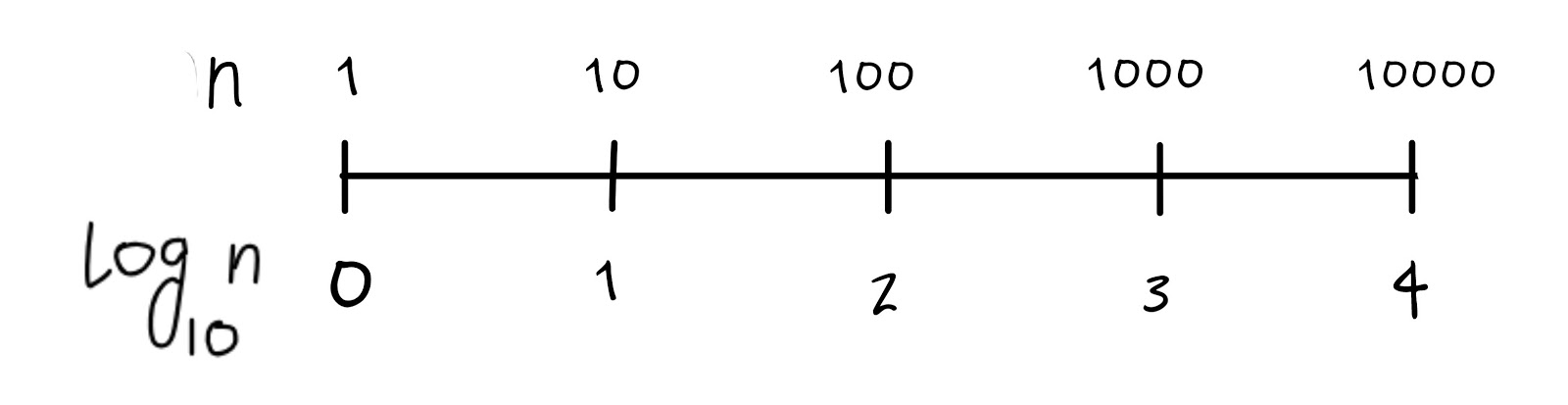
The points in this number line are multiples of 10.

Now, if we consider the floor value i.e 3 and add 1 to it, we get 4. Count the number of digits in 4591 yourself, it’s 4.

#include <stdio.h>
#include<math.h>
int count\_digits(int n){
    if(n==0)
        return 1;
    else
        return floor(log10(n)) + 1;
}
int main(void){
    int n;
    printf("Enter a no.: ");
    scanf("%d", &n);
    printf("Number of digits: %d", count\_digits(n));
 return 0;
}

It’s time to go mathematical #

References: #

It’s time to go mathematical
#

References:
#